Suivi de pendule
Contents
Génération des données
L = 400; % longueur de la séquence delta_t = 0.0002; % période d'échantillonnage omega_0 = 2*pi*50; % pulsation réelle (50 Hz) sigma_r = 0.5; % covariance du bruit de mesure T = (0:L) * delta_t; p0 = cos(omega_0*1 * T); z = p0 + sigma_r * randn(size(T)); % simulation des mesures
Définition du modèle d'évolution et du modèle de mesure
Le modèle d'évolution est obtenu par discrétisation du modèle physique continu.
Dans un premier temps, on suppose la pulsation parfaitement connue
sigma_q = 0.01; % covariance du bruit de modèle omega = omega_0; % pulsation modèle = pulsation réelle F = [cos(omega*delta_t), sin(omega * delta_t)/omega; - omega * sin(omega * delta_t), cos(omega*delta_t)]; % évolution du système H = [1 0]; % mesure de la position du pendule Q = sigma_q^2 * [0 0;0 1]; % bruit de modèle R = eye(1) * sigma_r^2; % bruit de mesure
Initialisation
On initialise à 0 avec une covariance élevée
x0 = [0; 0]; P0 = 1000*eye(2);
Filtre de Kalman
[xest, Pest] = kalman(z, F, H, Q, R, x0, P0);
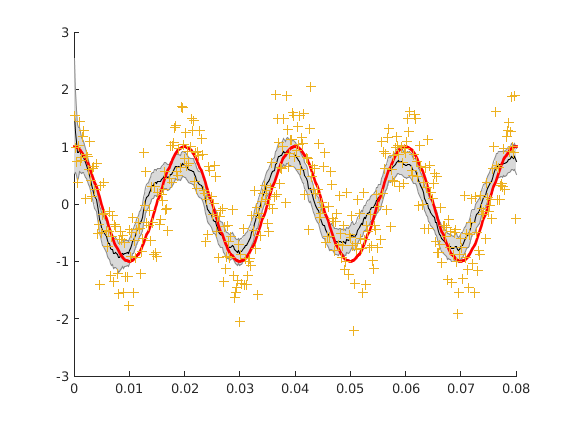
Estimation et intervalle de confiance à 95%
hold on shadedErrorBar(T, xest(1, :), 2*sqrt(squeeze(Pest(1, 1, :)))) plot(T, p0, 'r', 'linewidth', 2) plot(T, z, '+')
Estimation avec une pulsation erronée
On construit le modèle avec une pulsation surestimée de 20%
omega = 1.2 * omega_0;
F = [cos(omega*delta_t), sin(omega * delta_t)/omega;
- omega * sin(omega * delta_t), cos(omega*delta_t)]; % évolution du système
Filtre de Kalman
[xest, Pest, K] = kalman(z, F, H, Q, R, x0, P0);
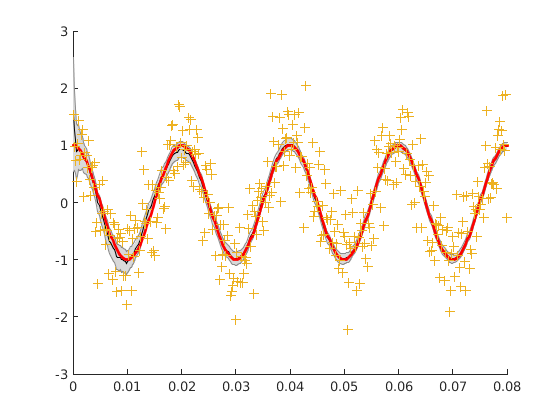
Estimation et intervalle de confiance
Le modèle est trop loin de la réalité, le filtre est incapable de donner une bonne estimation de la position du pendule
figure hold on shadedErrorBar(T, xest(1, :), 2*sqrt(squeeze(Pest(1, 1, :)))) plot(T, p0, 'r', 'linewidth', 2) plot(T, z, '+')
Pulsation érronée et fort bruit de modèle
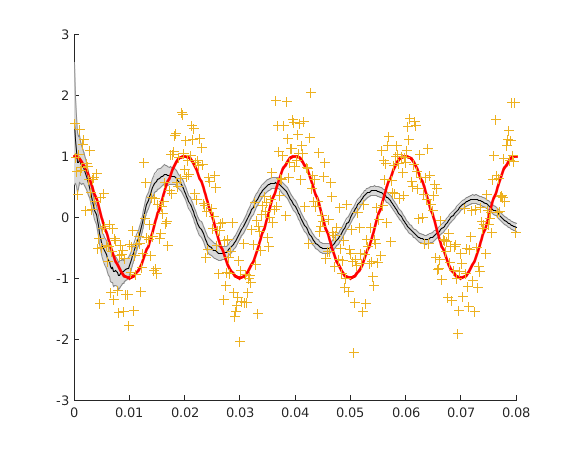
Dans ce cas, on peut fixer un bruit de modèle de variance élevée. L'estimation est bien sûr moins bonne que dans le cas où système et modèle sont accordés
sigma_q = 10; % covariance du bruit de modèle Q = sigma_q^2 * [0 0;0 1]; % bruit de modèle [xest, Pest, K] = kalman(z, F, H, Q, R, x0, P0); figure hold on shadedErrorBar(T, xest(1, :), 2*sqrt(squeeze(Pest(1, 1, :)))) plot(T, p0, 'r', 'linewidth', 2) plot(T, z, '+')