Estimation d'une constante avec le filtre de Kalman

Contents

Définition des paramètres

sigmaq = 0.001; % écart type du bruit de modèle
sigmar = 0.5; % écart type du bruit de mesure

F = 1; % matrice d'évolution, constante, pas d'évolution
H = 1; % mesure directe de l'état
Q = sigmaq^2; % covariance du bruit de modèle
R = sigmar^2; % covariance du bruit de mesure

Simulation des mesures

L = 200; % longueur de la séquence
z = 1 * ones(1, L) + sigmar * randn(1, L); % constante + du bruit

Filtre de Kalman

[xest, Pest, K] = kalman(z(2:end), F, H, Q, R, z(1), R);

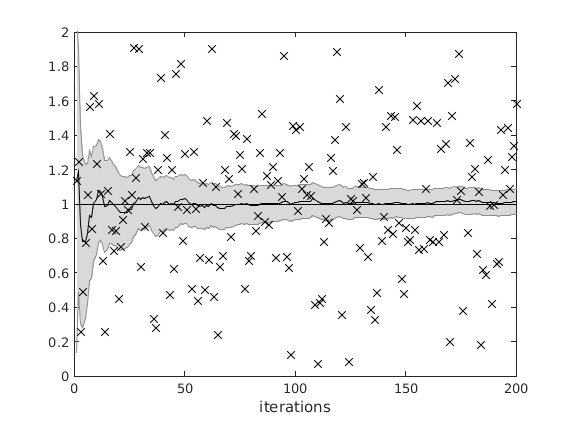
Tracé de l'estimation avec son intervalle de confiance à 95%

Xe = [z(1) xest(1,:)];

shadedErrorBar(1:L,Xe, 2*sqrt([R; squeeze(Pest)]))


hold on

plot(ones(L,1), 'k')
scatter(1:L,z, 'k', 'x')
xlim([0 L])
ylim([0 2])
xlabel('iterations')

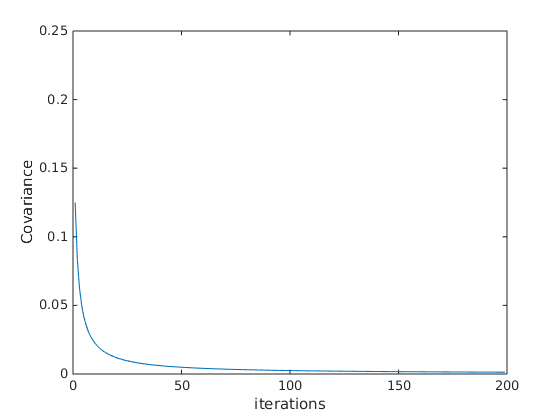
Variance de l'estimation

Au fur et à mesure des itérations, la variance de l'estimation diminue

figure
plot(squeeze(Pest))
xlim([0 L])
ylim([0 sigmar^2])
xlabel('iterations')
ylabel('Covariance')

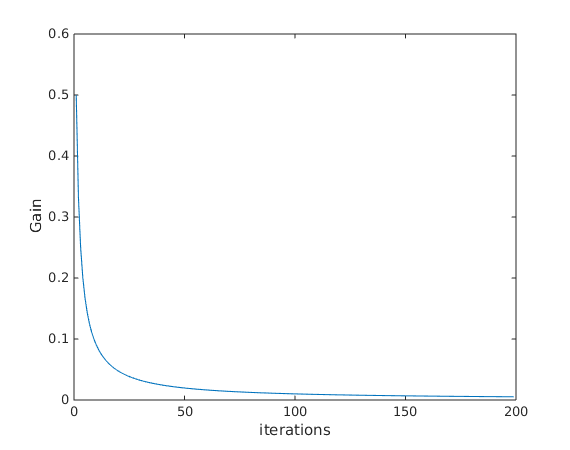
Gain de Kalman

Plus la variance de l'estimation est faible, plus le filtre de Kalman fait confiance au modèle. Ceci se traduit par un gain de Kalman de plus en plus faible.

figure
plot(squeeze(K))
xlim([0 L])
ylim([0 0.6])
xlabel('iterations')
ylabel('Gain')

Published with MATLAB® R2014b